Ray tracing in one weekend折射公式

本文是对Ray Tracing in One Weekend中折射一节公式的推导

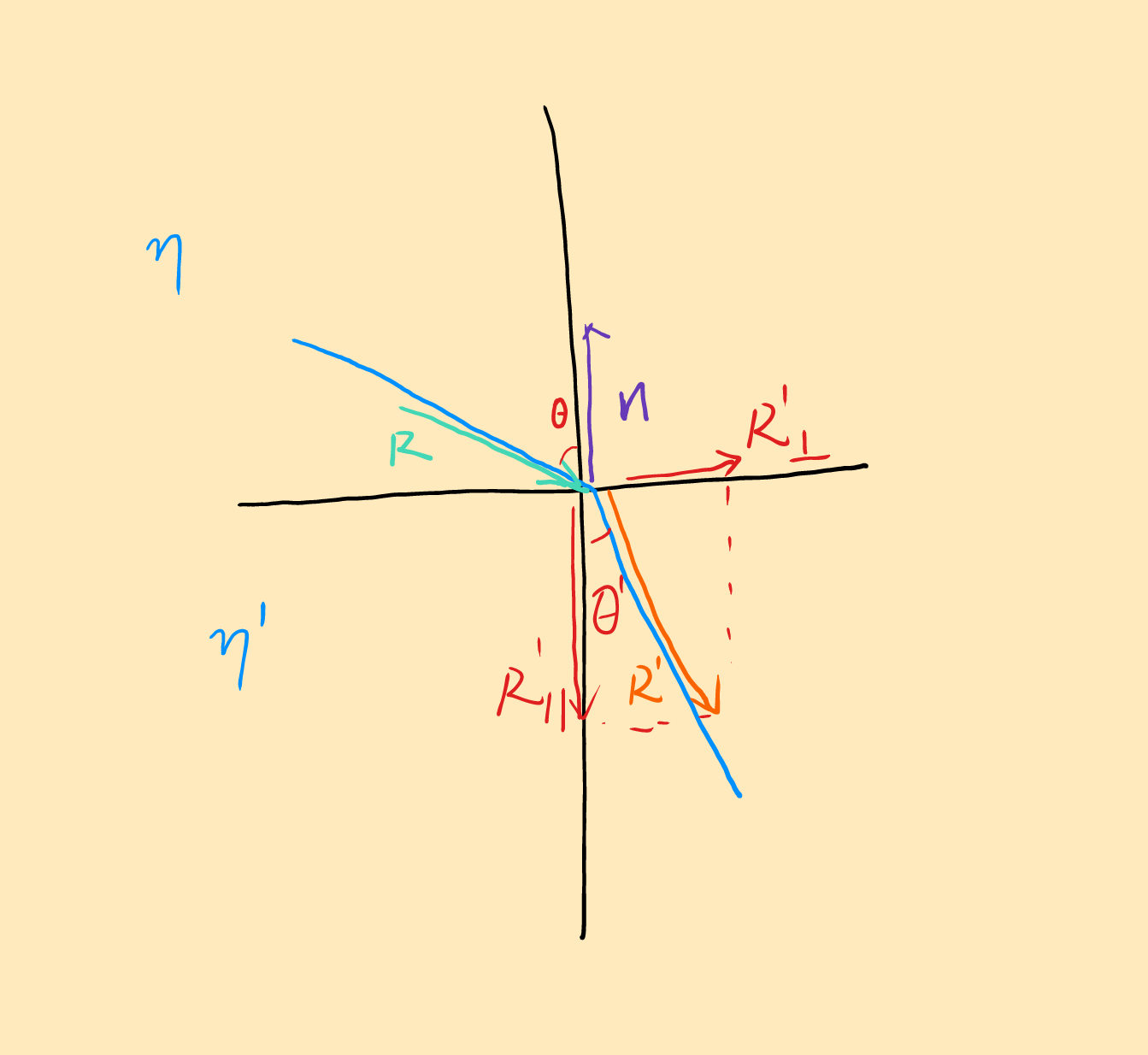
图中已知的变量已经用蓝色标出，分别是$\eta、\eta^{\prime}$，还有一个向量$R$已知，标为了绿色

图中一些向量为了方便观看用不同颜色标记了，其中$R_{\bot}^{\prime}$和$R_{\parallel}^{\prime}$是$R^{^{\prime}}$的分量，分别和法线$n$单位向量垂直和平行，$R$是入射光线与$R^{\prime}$出射光线两个向量都是单位向量，长度是1

首先要算出来的是$cos\theta$的值，因为$R$和$n$是单位向量，所以很容易得出

$$ \cos\theta = -R \cdot n$$

之后能看出$R$在y轴上的投影的长度为$R$的长度乘上$\cos\theta$，而$R$的长度和$n$的长度其实是一样的，所以也等于$n$的长度乘上$\cos\theta$，可以得出$R$在x轴上的分量为$R + n \cdot \cos\theta$，而这个分量的长度也容易通过图像得知是$\sin\theta$，所以x轴正方向的单位向量可以算出来是

$$\frac{R + n \cdot \cos\theta}{\sin\theta}$$

观察图像其实可以因为$R^{^{\prime}}$长度是1知道$R_{\bot}^{^{\prime}}$的长度是$\sin\theta^{^{\prime}}$

由于斯涅尔折射定律

$$ \sin\theta^{\prime} = \frac{\eta}{\eta^{\prime}} \cdot \sin\theta $$

可以得出

$$ R_{\bot}^{^{\prime}} = \sin\theta^{\prime} \cdot \frac{R + n \cdot \cos\theta}{\sin\theta} = \frac{\eta}{\eta^{\prime}} \cdot (R + n \cdot \cos\theta) = \frac{\eta}{\eta^{\prime}} \cdot (R + (-R \cdot n)n)$$

因为$R_{\parallel}^{\prime}$和$R_{\bot}^{\prime}$是垂直的，并且是同一个单位向量的分量，可以得出$R_{\parallel}^{\prime}$的长度为$ \sqrt{1 - |\mathbf{R^{\prime}}_{\bot}|^2}$，而$R_{\parallel}^{\prime}$的方向和$n$相反，所以

$$R_{\parallel}^{\prime} = -\sqrt{1 - |\mathbf{R}^{\prime}_{\bot}|^2} \cdot n$$

$R_{\parallel}^{\prime}$和$R_{\bot}^{\prime}$加起来就得到$R^{\prime}$了